Simple series resonance
Resonance, series LC Series LC resonanceA similar effect happens in series inductive/capacitive circuits. When a state of resonance is reached (capacitive and inductive reactances equal), the two impedances cancel each other out and the total impedance drops to zero!

At 159.155 Hz the following values are valid:
ZL = 0 + j100 W
ZC = 0 - j100 W
Zseries = ZC + ZL
Zseries = 0 - j100 W + 0 + j100 W = 0 W
With the total series impedance equal to 0 W at the resonant frequency of 159.155 Hz, the result is a short circuit across the AC power source at resonance. In the circuit drawn above, this would not be good. I'll add a small resistor in series along with the capacitor and the inductor to keep the maximum circuit current somewhat limited, and perform another SPICE analysis over the same range of frequencies:
 |  Download the circuit |
series lc circuit
v1 1 0 ac 1 sin
r1 1 2 1
c1 2 3 10u
l1 3 0 100m
.ac lin 20 100 200
.plot ac i(v1)
.end

As before, circuit current amplitude increases from left to right, while frequency increases from top to bottom. The peak is still seen to be at the plotted frequency point of 157.9 Hz, the closest analyzed point to our predicted resonance point of 159.155 Hz. This would suggest that our resonant frequency formula holds as true for simple series LC circuits as it does for simple parallel LC circuits, which is the case:
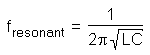
A word of caution is in order with series LC resonant circuits: because of the high currents which may be present in a series LC circuit at resonance, it is possible to produce dangerously high voltage drops across the capacitor and the inductor, as each component possesses significant impedance. We can edit the SPICE netlist in the above example to include a plot of voltage across the capacitor and inductor to demonstrate what happens:
series lc circuit
v1 1 0 ac 1 sin
r1 1 2 1
c1 2 3 10u
l1 3 0 100m
.ac lin 20 100 200
.plot ac i(v1) v(2,3) v(3)
.end

According to SPICE, the voltage across the capacitor and inductor reach a peak somewhere above 70 volts. This is quite impressive for a power supply that only generates 1 volt. Needless to say, caution is in order when experimenting with circuits such as this.
- REVIEW:
- The total impedance of a series LC circuit approaches zero as the power supply frequency approaches resonance.
- The same formula for determining resonant frequency in a simple tank circuit applies to simple series circuits as well.
- Extremely high voltages can be formed across the individual components of series LC circuits at resonance, due to high current flows and substantial individual component impedances.




































No comments:
Post a Comment